Voor het uitleggen van heel ingewikkelde concepten heeft Jenny Hasenack allerlei metaforen en vergelijkingen achter de hand. Maar toen ze het begrip ‘kwadraat’ moest uitleggen, bleek dat ongekend lastig.
Als wetenschapscommunicator denk ik veel na over het uitleggen van ingewikkelde concepten op een eenvoudige manier. Ik heb al behoorlijk moeilijke termen vertaald in metaforen, opgebroken in kleine stapjes of vereenvoudigd zodat een middelbare scholier ze zou kunnen snappen. Met het uitleggen van magnetische resonantie, electron holes of molecuulorbitaaltheorie kwam ik er meestal wel uit – gegeven dat de luisteraar enigszins geïnteresseerd was. Maar ‘Wat is een kwadraat?’ is de moeilijkste vraag die ik ooit heb moeten beantwoorden.
In de laatste lockdown heb ik, omdat mijn workshops en optredens waren gecanceld, mijn oude studentenbaantje weer opgepakt: bijles geven. Ik deed dat voornamelijk zodat ik in die eindeloze coronadagen iets te doen had, maar het bracht me veel meer dan ik van tevoren had verwacht. Met name dus omdat bleek dat mijn allereerste bijlesleerling vragen stelde bij de meest basale dingen – hij wist oprecht niet hoe een kwadraat werkte.
Hoe leg je uit wat een kwadraat is? Of eigenlijk: hoe leg je iets uit dat zo eenvoudig is dat je er nog nooit over na hebt gedacht? Voor electron holes kan ik zo een paar leuke verhalen of tekeningen uit de kast trekken, maar een kwadraat is ‘een getal keer zichzelf’. Als die uitleg niet werkt kun je dat niet eenvoudiger maken. Lezers die lesgeven op een middelbare school zullen dit probleem zeker herkennen, maar voor mij was het nieuw. Het voelde een beetje alsof ik een fundamenteel deeltje in tweeën probeerde te splitsen – je kunt het niet in stapjes opdelen. Het is één stap.
Vooral 22 gooide roet in het eten – hij extrapoleerde vanaf daar dat een kwadraat dan waarschijnlijk betekende dat 32 = 6, 42 = 8, enzovoort. Het lastige was ook dat met elke gefaalde uitleg, mijn leerling zich dommer ging voelen, wat het leerproces niet ten goede kwam. Ik moet toegeven dat ik zelf ook even in de val trapte – dat ik dacht ‘Hoe kun je dit nou nog niet begrijpen?’
Uiteindelijk zette ik me daar overheen. Ik heb hem, in plaats van een metafoor of uitgebreide uitleg, rijen en rijen aan kwadraatsommetjes laten doen en na een tijdje viel het kwartje. Het werkte om af te stappen van het idee dat je het wel móét begrijpen als je het makkelijk uitlegt. Als ik nu een wetenschapper advies geef hoe een bepaalde term uit te leggen, denk ik altijd terug aan de kwadraatjongen. Het is zo makkelijk te vergeten, maar soms moet je echt die ene fundamentele stap opdelen in honderd kleine stapjes.









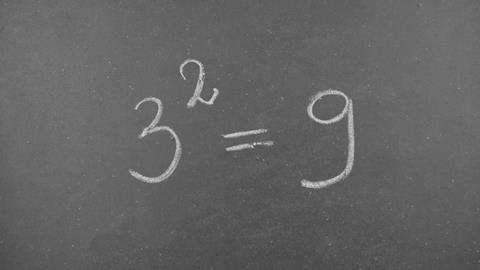










Nog geen opmerkingen